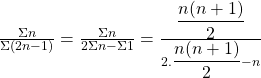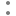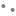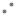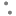
TS Polycet (Polytechnic) 2015 Previous Question Paper with Answers And Model Papers With Complete Analysis

TS Polycet (Polytechnic) 2015 Previous Question Paper with Answers And Model Papers With Complete Analysis
TS Polycet (Polytechnic) Previous Year Question Papers And Model Papers:
While preparing for TS Polycet (Polytechnic), candidates must also refer to the previous year question papers of the same. Scoring well in TS Polycet (Polytechnic) and understanding weaknesses and strengths in the respective sections.

TS Polycet (Polytechnic) Previous Year Question Papers can be found on this page in PDF format. Students taking the exam to get into some of the best Polytechnic colleges/institutes in the state of Andhra Pradesh may practice these papers to get a clear idea of the structure of the exam, marking scheme, important topics, etc.

TS Polycet Mock Test

Section — I
MATHEMATICS

Polycet 2015 Physics

Polycet 2015 Chemistry

Q). The sum of two numbers is 1000 and the difference between their squares is 256000. Find the numbers.
A) 630,370
B) 628,372
C) 626,374
D) 620,380

View Answer

B) 628,372
Explanation: Let the two numbers are x, y.
Given that x + y = 1000 ……….(1)
x² — y² = 256000
(x—y) (x + y)= 256000 (x-y) (1000) = 256000
x-y= 256 ……………………(2)
Solve(1)&(2)
x + y = 1000
x – y = 256
2x = 1256
⇒ x = 628
(1) ⇒ 628 + y = 1000
∴ y = 1000 – 628 ⇒ y = 372
∴ x = 628, y = 372

Q). Solve : 141x + 93y = 189, 93x+ 141y=45
A) (0,7)
B) (1,-1)
C) (1,2)
D) (2,-1)

View Answer

D) (2,-1)
Explanation: 141x + 93y=189 ………………….(1)
93x + 141y = 45 …………………(2)
Solve (1), (2)
$\frac x{-4185\;+\;26649}+\frac y{-17577\;+\;6345}+\frac1{19881-8649}$

x/22464 = y/-11232 = 1/11232
∴x = 2, y = – 1
∴ (x, y) = (2, – 1)

Q). If the system of equations 2x + 3y = 7, 2ax + (a + b) y = 28 has infinitely many solutions, then
A) a = 2b
B) b = 2a
C) a + 2b = 0
D) 2a + b = 0

View Answer

B) b = 2a
Explanation: a₁/a₂ = b₁/b₂ = c₁/c₂
⇒2/2a = 3/a+b = -7/-28
⇒1/a = 3/a+b = 1/4
⇒1/a = 1/4 ⇒a=4
∴3/a+b = 1/4⇒a+b =12
⇒4+b =12
⇒B = 8
∴b = 8 = 2(4) = 2a
∴b = 2a

Q). The squares of two consecutive integers differ by 13, then the largest integer is
A) 12
B) 6
C) 7
D) 13

View Answer

C) 7
Explanation: Let the two consecutive integers are x, x + 1.
Given that
(X+1)² = x² = 13
x²+ 1 +2x- x²= 13
1 + 2x = 13
2x = 12 ⇒ x = 6
∴ Largest integer = x+ 1 = 6+ 1 = 7.

Q). If 2x -3/x = 5, then x =
A) 1/2 ,3
B) -1/2, -3
C) -1/2, 3
D) 1/2, -3

View Answer

C) -1/2, 3
Explanation: 2x- 3/x = 5
2 x²-3/x = 5
2 x² – 3 = 5x
⇒ 2 x² – 5x -3 = 0 ⇒ 2 x²-6x + x- 3 = 0
⇒ 2x(x-3) + 1(x-3) = 0 ⇒ (2x + 1) (x-3) = 0
∴ x = 3 or x = -1/2

Q). If a x² + bx + c is a perfect square, then b²=
A) 4ac
B) ac
C) 2ac
D) √2ac

View Answer

A) 4ac
Explanation: a x² + bx + c is a perfect square then b² = 4ac

Q). If nth terms of the progressions 63, 65,67,……………….. and 3, 10, 17,……………….. are same, then n =
A) 10
B) 11
C) 12
D) 13

View Answer

D) 13
Explanation: I progression.: n^th term a_n = a + (n – 1) d
= 63+(n-1)2
= 63 + 2n — 2 = 2n + 61
II progression: n^th term a_n = a + (n – 1) d = 3 + (n – 1) 7
= 3 + 7n-7 = 7n – 4
Given that 2n + 61 = 7n – 4
7n-2n = 61 +4
5n = 65 ⇒ n = 13

Q). If a, b and c are in AP and a > 0, then…………………..are in GP.
A) a^a, b^b, c^c
B) a^c, b^a, c^b
C) a^b, b^c, c^a
D) a^a, a^b, a^c

View Answer

D) a^a, a^b, a^c
Explanation: a, b, c are in AP ⇒ 2b = a + c
a^2b = a^a+c
(ab)² = a^a .a^c
a^a, a^b, a^c are in G.P.

Q). In a GP, third-term is 24 and sixth-term is 192, then tenth-term is
A) 3072
B) 2456
C) 1346
D) 3126

View Answer

A) 3072
Explanation: t₃ = 24 ⇒ ar² = 24 …………………….(1)
t₆ = 192 ⇒ ar⁵ = 192 ………………………. (2)
(2)/(1) ⇒ ar⁵/ar² = 192/24
⇒ r³ = 8⇒ r = 2
(1) ⇒ a(2)² = 24 ⇒ 4a = 24 ⇒ a = 6
t₁₀ = ar⁹ = 6(2)⁹ = 3072

Q). $\frac{1+2+3+..................+n}{1+3+5+....+(2n-1)}$
A) $\frac{n+1}2$
B) $\frac{n+1}{2n}$
C) n(n+1)
D) None

View Answer

B) $\frac{n+1}{2n}$

Explanation: $\frac{1+2+3+..................+n}{1+3+5+....+(2n-1)}$

= $\frac{\Sigma n}{\Sigma(2n-1)}=\frac{\Sigma n}{2\Sigma n-\Sigma1}=\frac{\displaystyle\frac{n(n+1)}2}{\bcancel2.{\displaystyle\frac{n(n+1)}{\bcancel2}}-n}$

= 1/2 + 1/2n = n+1/2n

Spread the love

Section — I MATHEMATICS

Leave a Comment Cancel reply

Section — I
MATHEMATICS