AP Polycet (Polytechnic) 2022 Previous Question Paper with Answers And Model Papers With Complete Analysis

Polycet Mock Test

31) If a point P is 17cm from the center of a circle of radius 8cm, then the length of the tangent drawn to the circle from the point P is

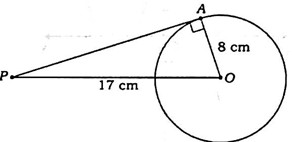
A) 10cm
B) 12cm
C) 15cm
D) 14cm

View Answer

C) 15cm

Explanation:Given: Distance from point P to center = 17 cm, Radius of circle = 8 cm
We use the Pythagorean theorem for the right triangle formed by radius, tangent, and line from P to center.
Let tangent length = t
$t^2 = 17^2 - 8^2 = 289 - 64 = 225 ⇒ t = \sqrt{225} = \boxed{15 \text{ cm}}$

32) If cos A= $\frac45$ , then the value of tan A is

A) $\frac35$
B) $\frac34$
C) $\frac43$
D) $\frac53$

View Answer

B) $\frac34$

Explanation:Given: $\cos A = \frac{4}{5}$
Use identity: $\sin^2 A + \cos^2 A = 1 ⇒ \sin A = \sqrt{1 - \left(\frac{4}{5}\right)^2} = \frac{3}{5}$
$\tan A = \frac{\sin A}{\cos A} = \frac{3/5}{4/5} = \boxed{\frac{3}{4}}$

33) The value of $\frac{cot45^\circ}{\sin\left(30^\circ\right)+\cos\left(60^\circ\right)}$ is equal to

A) 1
B) $\frac1{\sqrt2}$
C) $\frac23$
D) $\frac12$

View Answer

A) 1

$\cot 45^\circ = 1, \quad \sin 30^\circ = \frac{1}{2}, \quad \cos 60^\circ = \frac{1}{2}$
$\frac{\cot 45^\circ}{\sin 30^\circ + \cos 60^\circ} = \frac{1}{\frac{1}{2} + \frac{1}{2}} = \frac{1}{1} = \boxed{1}$

34) The value of tan 2°. tan 4°.tan 6°…tan 88° is

A) 0
B) 1
C) 2
D) Not defined

View Answer

B) 1

Explanation:This is a known trigonometric product:
$\tan 2^\circ \cdot \tan 4^\circ \cdot \tan 6^\circ \cdots \tan 88^\circ = \boxed{1}$

35) If tanθ+cotθ=5, then tan²θ+cot²θ=?

A) 27
B) 25
C) 24
D) 23

View Answer

D) 23

Explanation:Given: $\tan \theta + \cot \theta = 5$
Use identity:
$(\tan \theta + \cot \theta)^2 = \tan^2 \theta + \cot^2 \theta + 2 ⇒ 25 = \tan^2 \theta + \cot^2 \theta + 2 ⇒ \tan^2 \theta + \cot^2 \theta = 25 - 2 = \boxed{23}$

Spread the love

Leave a Reply Cancel reply