AP Polycet (Polytechnic) 2022 Previous Question Paper with Answers And Model Papers With Complete Analysis

Authoradmin / Posted onLeave a comment

Polycet Mock Test

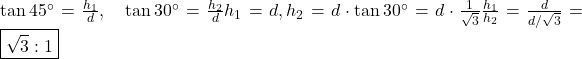
36) If x=asinθ and y=btanθ, then the value of \frac{a^2}{x^2}-\frac{b^2}{y^2} is

A) 1
B) 2
C) -1
D) None of these

View Answer
A) 1

Explanation:Given: x = a \sin \theta, y = b \tan \theta
Then:
\frac{a^2}{x^2} = \frac{1}{\sin^2 \theta}, \quad \frac{b^2}{y^2} = \frac{1}{\tan^2 \theta} = \frac{\cos^2 \theta}{\sin^2 \theta} ⇒ \frac{a^2}{x^2} - \frac{b^2}{y^2} = \frac{1 - \cos^2 \theta}{\sin^2 \theta} = \frac{\sin^2 \theta}{\sin^2 \theta} = \boxed{1}

37) If secθ+tanθ=x, then tan θ=

A) \frac{x^2+1}x
B) \frac{x^2-1}x
C) \frac{x^2+1}{2x}
D) \frac{x^2-1}{2x}

View Answer
D) \frac{x^2-1}{2x}

Explanation:Given: \sec \theta + \tan \theta = x
Use identity:
(\sec \theta + \tan \theta)^2 = \sec^2 \theta + \tan^2 \theta + 2 \sec \theta \tan \theta = x^2 ⇒ 1 + \tan^2 \theta + \tan^2 \theta + 2 \tan \theta \sqrt{1 + \tan^2 \theta} = x^2
Too long—use shortcut:
From identity:
\tan \theta = \frac{x^2 - 1}{2x}

38) \frac{\sin\left(\theta\right)}{1+\cos\left(\theta\right)}=

A) \frac{1+\cos\left(\theta\right)}{\sin\left(\theta\right)}
B) \frac{1-\cos\left(\theta\right)}{\cos\left(\theta\right)}
C) \frac{1-\cos\left(\theta\right)}{\sin\left(\theta\right)}
D) \frac{1+\sin\left(\theta\right)}{\cos\left(\theta\right)}

View Answer
C) \frac{1-\cos\left(\theta\right)}{\sin\left(\theta\right)}

Explanation:Use identity:
\frac{\sin \theta}{1 + \cos \theta} = \frac{1 - \cos \theta}{\sin \theta} \quad \text{(rationalizing)}
Answer:\frac{1 - \cos \theta}{\sin \theta}

39) If the ratio of the length of a pole and its shadow is 1:√3, then the angle of elevation of the

A) 30°
B) 45°
C) 60°
D) 90°

View Answer
C) 60°

Explanation:Pole\:Shadow = 1:√3 → Use basic trigonometry:
\tan \theta = \frac{\text{opposite}}{\text{adjacent}} = \frac{1}{\sqrt{3}} ⇒ \theta = \boxed{30^\circ}

40) If two towers of heights h1 and h2 subtend angles 45° and 30° respectively at the midpoint of the line joining their feet, then the ratio of h1: h2 is

A) 1:√3
B) √3:1
C) 1:3
D) 3:1

View Answer
B) √3:1

Explanation:Use:
\tan 45^\circ = \frac{h_1}{d}, \quad \tan 30^\circ = \frac{h_2}{d} ⇒ h_1 = d, h_2 = d \cdot \tan 30^\circ = d \cdot \frac{1}{\sqrt{3}} ⇒ \frac{h_1}{h_2} = \frac{d}{d/\sqrt{3}} = \boxed{\sqrt{3}:1}

Spread the love

Leave a Reply