TS Polycet (Polytechnic) 2021 Previous Question Paper with Answers And Model Papers With Complete Analysis

Polycet Mock Test

26) The distance between the points (0, 0) and (5,12) is

A) 11
B) 12
C) 13
D) 14

View Answer

C) 13

Explanation:Distance between (0, 0) and (5, 12) is:
$\sqrt{(5-0)^2 + (12-0)^2} = \sqrt{25 + 144} = \sqrt{169} = 13$

27) If the slope of the line through (x,5) and (5,2) is 3, then the value of x is

A) 3
B) 4
C) 5
D) 6

View Answer

D) 6

Explanation:Slope of the line through (x, 5) and (5, 2) is 3. Find (x):
$\text{Slope} = \frac{2 - 5}{5 - x} = 3 ⇒ \frac{-3}{5 - x} = 3 ⇒ -3 = 15 - 3x ⇒ x = 6$

28) If △ABC~△PQR, ∠A=32°, ∠R=65° then ∠B=

A) 93°
B) 83°
C) 73°
D) 63°

View Answer

B) 83°

Explanation:If (ΔABC ~ ΔPQR), (∠A = 32°), (∠R = 65°), then (∠B = ?)
Corresponding angles are equal, so (∠C = ∠R = 65°).
Sum of angles in (ΔABC) :
∠B = 180° – ∠A – ∠C = 180° – 32° – 65° = 83°

29) The angle in the minor segment is

A) obtuse
B) acute
C) 90°
D) None of these

View Answer

A) obtuse

Explanation:The angle in the minor segment is:
An angle in the minor segment is obtuse(greater than (90°).

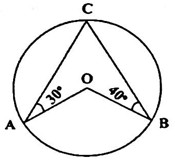
30) In the figure ∠BAO=30°, ∠BCO=40° then ∠AOC=

A) 100°
B) 120°
C) 140°
D) 150°

View Answer

C) 140°

Explanation:In the figure, (∠BAO = 30°), (∠BCO = 40°). Then (∠AOC = ?)
From the figure (assuming (O) is the center of the circle):
– (∠AOC = 2(∠ABC) (Central angle theorem).
– (∠ABC = ∠BAO + ∠BCO = 30° + 40° = 70°).
– Thus, (∠AOC = 2 × 70° = 140°).

Spread the love

Leave a Reply Cancel reply