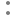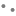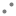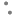
46) If ![]() where a1x+b1y+c1=0 and a2x+b2y+c2=0 are two linear equations,
where a1x+b1y+c1=0 and a2x+b2y+c2=0 are two linear equations, ![]()
![]()
![]()
A) have a unique solution ఏకైక సాధన కలిగి ఉంటాయి
B) have infinitely many solutions అనంతమైన సాధనలు కలిగి ఉంటాయి
C) have finite solutions పరిమితమైన సాధనలు కలిగి ఉంటాయి
D) have no solution ఏ సాధనలను కలిగి ఉండవు
47) The value of p, for which the pair of equations 3x+4y+2=0 and 9x+ py+8=0 represents parallel lines, is 3x +4y+ 2 = 0 మరియు 9x + py + 8 = 0 అను సమీకరణాల జత సమాంతర రేఖలను సూచించిన, P విలువ
A) 2
B) 4
C) 6
D) 12
48) Which of the following equation represent the situation where Kiran bought 5 oranges, 7 apples and Harish bought 2 oranges, 12 apples for same amount of total money? కిరణ్ 5 నారింజలు, 7 యాపిల్స్ మరియు హరీశ్ 2 నారింజలు, 12 యాపిల్స్ విడివిడిగా ఒకే మొత్తానికి కొన్నారు. కింది సమీకరణాలలో ఈ విషయాన్ని సూచించే సమీకరణము ఏది?
A) 5x+12y=2x+7y
B) 5x+7y=2x+12y
C) 5x-7y=2x-12y
D) 5x+2y=7x+12y
49) If ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A) x=4, y=3
B) x=2, y=9
C) x=4, y=9
D) x=2, y=3
50) The pair of equations x+y=5 and 2x+2y=k has infinitely many solutions if k = x + y = 5 మరియు 2x + 2y = k అను సమీకరణాల జత అనంతమైన సాధనలను కలిగి ఉండాలి అనిన, k =
A) 4
B) 6
C) 8
D) 10