TS Polycet (Polytechnic) 2024 Previous Question Paper with Answers And Model Papers With Complete Analysis

Polycet Mock Test

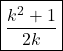
21) From a helicopter a person observes an object on the ground at an angle of depression 30°. If the helicopter is flying at a height of 500 m from the ground, then the distance between the person and the object is ఒక హెలికాప్టర్ నుండి ఒక వ్యక్తి భూమి పైనున్న ఒక వస్తువును 30° నిమ్నకోణంలో పరిశీలించాడు. భూమి పై నుండి హెలికాప్టర్ 500 మీ. ఎత్తులో ఎగురుతూ ఉంటే, వ్యక్తికి మరియు వస్తువుకు మధ్య దూరము

A) 500 m
B) 1000 m
C) $500\sqrt2\;m$
D) $\frac{500}{\sqrt3}m$

View Answer

B) 1000 m

Explanation:🎯 Shortcut Method Using Trigonometry (Hypotenuse Calculation)
We are given:
– The angle of depression from the helicopter to the object on the ground is $30^\circ$ .
– The height of the helicopter from the ground is 500 meters.
We need to find the distance between the person and the object (which is the hypotenuse of the right triangle formed by the height, the distance on the ground, and the line of sight).
Step 1: Using the Angle of Depression and Trigonometric Ratio
In this case, the angle of depression forms a right triangle with:
– The height of the helicopter as the opposite side (500 m),
– The distance between the person and the object as the hypotenuse,
– The horizontal distance between the object and the point on the ground directly beneath the helicopter as the adjacent side.
We can use the tangent function to relate the height and the horizontal distance first, then apply the cosine or sine to find the hypotenuse.
$\tan(30^\circ) = \frac{\text{height}}{\text{horizontal distance}}$
Since $\tan(30^\circ) = \frac{1}{\sqrt{3}}$ , we have:
$\frac{1}{\sqrt{3}} = \frac{500}{\text{horizontal distance}}$
Solving for the horizontal distance:
$\text{horizontal distance} = 500 \times \sqrt{3}$
Step 2: Apply the Pythagorean Theorem
Now, we can calculate the distance between the person and the object (the hypotenuse). We know:
– The height (opposite side) is 500 m,
– The horizontal distance (adjacent side) is $500 \times \sqrt{3}$ .
Using the Pythagorean theorem:
$\text{distance} = \sqrt{\left(500\right)^2 + \left(500\sqrt{3}\right)^2}$
$\text{distance} = \sqrt{500^2 + 500^2 \times 3}$
$\text{distance} = \sqrt{500^2(1 + 3)}$
$\text{distance} = \sqrt{500^2 \times 4}$
$\text{distance} = 500 \times \sqrt{4} = 500 \times 2 = 1000 \, \text{m}$
Final Answer: $\boxed{1000 \, \text{m}}$

22) The product of prime factors of 2024 is 2024 యొక్క ప్రధాన కారణాంకాల లబ్ధము

A) 11 × 23 × 3²
B) 23 × 11 × 2³
C) 7 × 23 × 2³
D) 23 × 112 × 2²

View Answer

B) 23 × 11 × 2³

Explanation:🎯 Shortcut Method to Find the Prime Factorization of 2024
We need to find the prime factorization of 2024.
Step 1: Start by dividing 2024 by the smallest prime (2):
$2024 \div 2 = 1012$
$1012 \div 2 = 506$
$506 \div 2 = 253$
Now, 253 is not divisible by 2, so we move to the next smallest prime, which is 3. However, 253 is not divisible by 3 either, so we check for divisibility by 5, and it’s not divisible by 5 either.
Step 2: Check divisibility by 11:
$253 \div 11 = 23$
23 is a prime number, so the prime factorization of 2024 is:
$2024 = 2^3 \times 11 \times 23$
Final Answer: $\boxed{23 \times 11 \times 2^3}$

23) {0} is a set which has ______ elements. {0} అనేది ______ మూలకాలను కలిగి ఉన్న సమితి.

A) 0
B) 1
C) 4
D) 3

View Answer

B) 1

Explanation:🎯 Explanation:
The set $\{0\}$ is a set containing a single element, which is $0$ .
So, the number of elements in the set $\{0\}$ is 1.
Final Answer: $\boxed{1}$

24) If cosec θ + cot θ = k, then the value of cosec θ is cos ec θ + cot θ = k అయిన, cosec θ యొక్క విలువ

A) $\frac{k^2+1}{2k}$
B) 0
C) $\frac{k^2-1}{k^2+1}$
D) $\frac1k$

View Answer

A) $\frac{k^2+1}{2k}$

Explanation:🎯 Shortcut Method to Find $\csc \theta$ in Terms of $k$
We are given that:
$\csc \theta + \cot \theta = k$
We need to express $\csc \theta$ in terms of $k$ .
Step 1: Use the identity for $\csc^2 \theta - \cot^2 \theta$
We know that:
$\csc^2 \theta = 1 + \cot^2 \theta$
Rearranging the given equation:
$\csc \theta = k - \cot \theta$
Now, we square both sides of this equation:
$\csc^2 \theta = (k - \cot \theta)^2$
Expanding the square:
$\csc^2 \theta = k^2 - 2k \cot \theta + \cot^2 \theta$
Using the identity $\csc^2 \theta = 1 + \cot^2 \theta$ , we substitute:
$1 + \cot^2 \theta = k^2 - 2k \cot \theta + \cot^2 \theta$
Step 2: Simplify the equation
Canceling out $\cot^2 \theta$ from both sides:
$1 = k^2 - 2k \cot \theta$
Rearranging:
$2k \cot \theta = k^2 - 1$
$\cot \theta = \frac{k^2 - 1}{2k}$
Step 3: Substitute $\cot \theta$ back into the equation for $\csc \theta$
Now, substitute $\cot \theta = \frac{k^2 - 1}{2k}$ back into $\csc \theta = k - \cot \theta$ :
$\csc \theta = k - \frac{k^2 - 1}{2k}$
Simplify the right-hand side:
$\csc \theta = \frac{2k^2 - (k^2 - 1)}{2k}$
$\csc \theta = \frac{k^2 + 1}{2k}$
Final Answer: $\boxed{\frac{k^2 + 1}{2k}}$

25) The value of $\log_6^2+\log_6^3$ is $\log_6^2+\log_6^3$ యొక్క విలువ

A) 0
B) 1
C) 2
D) 3

View Answer

B) 1

Explanation:🎯 Shortcut Method to Simplify the Expression $\log_6 2 + \log_6 3$
We are asked to simplify the expression:
$\log_6 2 + \log_6 3$
Step 1: Apply the logarithmic property of addition
We use the property of logarithms that states:
$\log_b x + \log_b y = \log_b (xy)$
So, applying this property:
$\log_6 2 + \log_6 3 = \log_6 (2 \times 3) = \log_6 6$
Step 2: Simplify $\log_6 6$
We know that:
$\log_b b = 1$
So:
$\log_6 6 = 1$
Final Answer: $\boxed{1}$