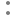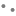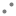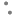
TS Polycet (Polytechnic) 2024 Previous Question Paper with Answers And Model Papers With Complete Analysis

Polycet Mock Test

31) Two boys on the either side of a temple of 45 meters height observe its top at the angles of elevation 30° and 60° respectively. Find the distance between the two boys? 45 మీ. ఎత్తుగల ఒక గుడి పై భాగాన్ని, దాని ఇరువైపులానున్న ఇద్దరు బాలురు 30° మరియు 60° ఊర్ధ్వకోణాలతో పరిశీలించారు. ఆ ఇద్దరు బాలుర మధ్య దూరం ఎంత?

A) 60√3 m
B) 40√3 m
C) $\frac{60}{\sqrt3}m$
D) $\frac{40}{\sqrt3}m$

View Answer

A) 60√3 m

Explanation:🎯 Shortcut Method to Find the Distance Between Two Boys
We are given:
– Height of the temple $h = 45 \, \text{m}$
– Angle of elevation from the first boy $\theta_1 = 30^\circ$
– Angle of elevation from the second boy $\theta_2 = 60^\circ$
The two boys are on opposite sides of the temple, and we need to find the distance between them.
Step 1: Use tan to relate the distances from each boy to the temple.
From the tan function:
– For the first boy:
$\tan 30^\circ = \frac{h}{d_1}$
where $d_1$ is the distance from the first boy to the temple.
$\tan 30^\circ = \frac{45}{d_1}$
Since $\tan 30^\circ = \frac{1}{\sqrt{3}}$ :
$\frac{1}{\sqrt{3}} = \frac{45}{d_1}$
$d_1 = 45 \sqrt{3}$
– For the second boy:
$\tan 60^\circ = \frac{h}{d_2}$
where $d_2$ is the distance from the second boy to the temple.
$\tan 60^\circ = \frac{45}{d_2}$
Since $\tan 60^\circ = \sqrt{3}$ :
$\sqrt{3} = \frac{45}{d_2}$
$d_2 = \frac{45}{\sqrt{3}} = 15\sqrt{3}$
Step 2: Find the total distance between the two boys.
The total distance between the two boys is the sum of $d_1$ and $d_2$ :
$\text{Distance between the two boys} = d_1 + d_2 = 45 \sqrt{3} + 15 \sqrt{3} = 60 \sqrt{3}$
Final Answer: $\boxed{60\sqrt{3} \, \text{m}}$

32) If a cylinder and a cone have bases of equal radii and are of equal heights, then that their volumes are in the ratio of _____ ఒక స్థూపము మరియు శంఖువు సమాన భూవ్యాసార్ధమును మరియు ఎత్తును కల్గి ఉన్నాయి. అయినచో, వాటి ఘనపరిమాణముల నిష్పత్తి_____.

A) 1:2
B) 2:3
C) 3:1
D) 1:4

View Answer

C) 3:1

Explanation:🎯 Shortcut Method to Find the Volume Ratio of a Cylinder and a Cone
Given:
– The radius of the base ( $r$ ) and the height ( $h$ ) of both the cylinder and the cone are equal.
Volume Formula for Cylinder:
$V_{\text{cylinder}} = \pi r^2 h$
Volume Formula for Cone:
$V_{\text{cone}} = \frac{1}{3} \pi r^2 h$
Finding the Ratio of Volumes:
The ratio of the volume of the cylinder to the volume of the cone is:
$\frac{V_{\text{cylinder}}}{V_{\text{cone}}} = \frac{\pi r^2 h}{\frac{1}{3} \pi r^2 h}$
Simplifying the expression:
$\frac{V_{\text{cylinder}}}{V_{\text{cone}}} = 3$
Thus, the volume of the cylinder is 3 times the volume of the cone.
Final Answer: $\boxed{3:1}$

33) If two cubes each of volume 64 cm3 are joined end to end together, then the surface area of the resulting cuboid is ____. 64 ఘనపు సెం.మీ. ఘనపరిమాణము గల రెండు సమఘనములు అంచులు తాకునట్లు అమర్చబడినవి. అయిన, ఏర్పడిన క్రొత్త ఘనాకృతి యొక్క సంపూర్ణతల వైశాల్యము ____.

A) 128 cm²
B) 160 cm²
C) 192 cm²
D) 384 cm²

View Answer

B) 160 cm²

Explanation:🎯 Shortcut Method to Find the Surface Area of a Cuboid
Given:
– Volume of each cube = $64 \, \text{cm}^3$
– The cubes are joined end to end to form a cuboid.
Step 1: Find the side length of each cube
The volume of a cube is given by the formula:
$V_{\text{cube}} = a^3$
Where $a$ is the side length of the cube.
For each cube: $64 = a^3$ Taking the cube root of both sides: $a = \sqrt[3]{64} = 4 \, \text{cm}$
So, the side length of each cube is $4 \, \text{cm}$ .
Step 2: Dimensions of the resulting cuboid
When the two cubes are joined end to end:
– The length of the cuboid = 4 + 4 = 8, cm
– The width of the cuboid = 4 cm (the same as the side of the cube)
– The height of the cuboid = 4cm (the same as the side of the cube)
Step 3: Surface Area of the Cuboid
The surface area A of a cuboid is given by the formula:
A = 2(lw + lh + wh)
Substitute the dimensions of the cuboid:
– l = 8cm
– w = 4cm
– h = 4cm
$A = 2 \left( (8 \times 4) + (8 \times 4) + (4 \times 4) \right)$
$A = 2 \left( 32 + 32 + 16 \right)$
$A = 2 \times 80 = 160 \, \text{cm}^2$
Final Answer: $\boxed{160 \, \text{cm}^2}$

34) If ABC is a right triangle right angled at ‘C’ and let BC = a, CA =b, AB = c and let p be the length of perpendicular from C on AB, then ________. లంబకోణ త్రిభుజము ABC లో లంబకోణము శీర్షము ‘C’’ వద్ద కలదు. BC= a, CA=b, AB= c మరియు ‘C’ నుండి AB కి గీసిన లంబము పొడవు p అయిన _____

A) cp = ab
B) $\frac1{p^2}=\frac1{a^2}-\frac1{b^2}$
C) $a^2+b^{2\;}=\;p^2$
D) None ఏదీ కాదు

View Answer

A) cp = ab

Explanation:🎯 Given Information:
– Triangle ABC is a right triangle right-angled at C.
– The sides of the triangle are:
– BC = a (perpendicular side),
– CA = b (perpendicular side),
– AB = c (hypotenuse).
– p is the length of the perpendicular from C on AB.
We need to identify the correct relationship involving $p$ , $a$ , $b$ , and $c$ .
Step 1: Using the Area of the Triangle
The area of the triangle can be calculated in two ways:
– 1. Using the base and height (since it’s a right triangle):
$\text{Area} = \frac{1}{2} \times a \times b$
– 2. Using the hypotenuse and the perpendicular p from C to the hypotenuse AB:
$\text{Area} = \frac{1}{2} \times c \times p$
Since both expressions represent the area of the same triangle, equating them gives us:
$\frac{1}{2} \times a \times b = \frac{1}{2} \times c \times p$
Simplifying:
$a \times b = c \times p$
Thus, the relationship is:
$\boxed{c \times p = a \times b}$

35) Two dice are thrown at the same time. What is the probability that the sum of the two numbers appearing on the top of the dice is 13? రెండు పాచికలు ఒకేసారి దొర్లించడం జరిగింది. రెండు పాచికలపై కనిపించే చుక్కల మొత్తం 13 అవ్వడానికి సంభావ్యత ఎంత?

A) 1
B) 1/2
C) 2/3
D) 0

View Answer

D) 0

Explanation:🎯 Understanding the Problem
We are rolling two dice and we need to find the probability that the sum of the numbers on the top of the dice is 13.
Step 1: Possible Outcomes when Rolling Two Dice
Each die has 6 faces, numbered from 1 to 6. Therefore, the total number of possible outcomes when two dice are rolled is:
$6 \times 6 = 36$
Step 2: Sum of 13
To get a sum of 13, let’s check the possible combinations:
– The highest sum you can get when rolling two dice is $6 + 6 = 12$ , which means it’s impossible to get a sum of 13.
Step 3: Conclusion
Since there is no way to get a sum of 13 with two dice, the number of favorable outcomes is 0.
Step 4: Calculating the Probability
The probability is calculated as:
$\text{Probability} = \frac{\text{Number of favorable outcomes}}{\text{Total number of outcomes}} = \frac{0}{36} = 0$
Final Answer:
$\boxed{0}$

Spread the love

Leave a Reply Cancel reply