TS Polycet (Polytechnic) 2024 Previous Question Paper with Answers And Model Papers With Complete Analysis

Polycet Mock Test

41) There are exactly _____ tangents to a circle through a point outside the circle. వృత్త బాహ్యంలో గల ఏదైనా బిందువు గుండా వృత్తానికి ఖచ్చితంగా _____ స్పర్శరేఖలు గీయగలము.

A) two
B) three
C) infinite
D) None

View Answer

A) two

42) The length of the tangent from a point 15 cm away from the centre of a circle of radius 9 cm is ____. 9 సెం.మీ. వ్యాసార్ధముగా గల వృత్తానికి దాని కేంద్రం నుండి 15 సెం.మీ. దూరములో ఒక బిందువు కలదు. అయిన, ఆ బిందువు నుండి వృత్తానికి గీయబడిన స్పర్శరేఖ పొడవు ______.

A) 15 cm
B) 13 cm
C) 11 cm
D) 12 cm

View Answer

D) 12 cm

Explanation:To find the length of the tangent from a point outside the circle, we can use the Pythagorean Theorem.
Given:
– The distance from the point to the center of the circle (the hypotenuse of the right triangle) = 15 cm.
– The radius of the circle (one leg of the right triangle) = 9 cm.
We need to find the length of the tangent, which is the other leg of the right triangle.
Using the Pythagorean theorem:
$\text{(distance from the point to the center)}^2 = \text{(radius)}^2 + \text{(length of the tangent)}^2$
Substitute the values:
$15^2 = 9^2 + \text{(length of the tangent)}^2$
$225 = 81 + \text{(length of the tangent)}^2$
$\text{(length of the tangent)}^2 = 225 - 81 = 144$
$\text{length of the tangent} = \sqrt{144} = 12 \, \text{cm}$
Final Answer:
The length of the tangent is 12 cm. So, the correct option is 4. 12 cm.

43) If the areas of two similar triangles are 81 cm² and 49 cm² respectively. If the altitude of the smaller triangle is 3.5 cm, then the corresponding altitude of the bigger triangle Is _____ రెండు సరూప త్రిభుజాల వైశాల్యలు 81 చ.సెం.మీ. మరియు 49 చ.సెం.మీ. చిన్న త్రిభుజములో గీసిన లంబము పొడవు 3.5 సెం.మీ. అయిన, పెద్ద త్రిభుజములో దాని అనురూప లంబము పొడవు ____

A) 9.5 cm
B) 9 cm
C) 7 cm
D) 4.5 cm

View Answer

D) 4.5 cm

Explanation:Given:
– Areas of two similar triangles = 81 cm² and 49 cm²
– Altitude of the smaller triangle = 3.5 cm
Formula:
For two similar triangles, the ratio of their areas is the square of the ratio of their corresponding sides (or altitudes).
$\frac{\text{Area of larger triangle}}{\text{Area of smaller triangle}} = \left(\frac{\text{Corresponding side of larger triangle}}{\text{Corresponding side of smaller triangle}}\right)^2$
Step 1: Find the ratio of the areas $\frac{81}{49} = \left(\frac{\text{Altitude of larger triangle}}{\text{Altitude of smaller triangle}}\right)^2$
$\left(\frac{\text{Altitude of larger triangle}}{\text{Altitude of smaller triangle}}\right)^2 = \frac{81}{49} = \left(\frac{9}{7}\right)^2$
$\frac{\text{Altitude of larger triangle}}{\text{Altitude of smaller triangle}} = \frac{9}{7}$
Step 2: Find the altitude of the larger triangle
Now, we can calculate the altitude of the larger triangle by multiplying the altitude of the smaller triangle by the ratio of the corresponding sides.
$\text{Altitude of larger triangle} = \text{Altitude of smaller triangle} \times \frac{9}{7}$
$\text{Altitude of larger triangle} = 3.5 \times \frac{9}{7} = 3.5 \times 1.2857 \approx 4.5 \, \text{cm}$
Final Answer:
The altitude of the larger triangle is 4.5 cm.

44) A tangent to a circle touches it in _____ point(s). వృత్తానికి గీయబడిన స్పర్శరేఖ దానిని ____ బిందువు(ల) వద్ద స్పృశిస్తుంది.

A) one
B) two
C) three
D) infinite
అనంత

View Answer

A) one

45) If AP and AQ are the two tangents to a circle with centre ‘O’, so that $\angle POQ\;=110^\circ$ , then $\angle PAQ$ = ______. క్రింది పటములో ‘O’ కేంద్రముగా గల వృత్తానికి, AP మరియు AQ లు రెండు స్పర్శరేఖలు మరియు $\angle POQ\;=110^\circ$ అయిన, $\angle PAQ$ = ________.

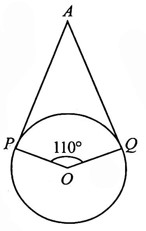
A) 60°
B) 70°
C) 80°
D) 90°

View Answer

B) 70°

Explanation:To find the measure of angle $\angle PAQ$ given that $\angle POQ = 110^\circ$ , we can use the properties of tangents to a circle and the fact that the sum of angles in a quadrilateral is $360^\circ$ .
Given:
– $AP$ and $AQ$ are tangents to the circle with center $O$ .
– $\angle POQ = 110^\circ$ .
Key Properties:
– 1. Tangents are perpendicular to the radius at the point of contact:
– $\angle OAP = 90^\circ$ (since $AP$ is a tangent and $OA$ is the radius).
– $\angle OAQ = 90^\circ$ (since $AQ$ is a tangent and $OA$ is the radius).
– 2. Sum of angles in quadrilateral $APOQ$ :
$\angle OAP + \angle APO + \angle POQ + \angle OAQ = 360^\circ$
Substituting the known values:
$90^\circ + \angle APO + 110^\circ + 90^\circ = 360^\circ$
Simplifying:
$\angle APO = 360^\circ - 290^\circ = 70^\circ$
– 3. Since $AP = AQ$ (tangents from an external point are equal), triangle $APQ$ is isosceles:
$\angle PAQ = 180^\circ - 2 \times \angle APO = 180^\circ - 2 \times 70^\circ = 40^\circ$
However, let’s verify this with a more straightforward approach.
Alternative (Simpler) Approach:
– The angle between two tangents ( $\angle PAQ$ ) is related to the angle subtended at the center ( $\angle POQ$ ) by:
$\angle PAQ = 180^\circ - \angle POQ$
Substituting the given value:
$\angle PAQ = 180^\circ - 110^\circ = 70^\circ$
Final Answer: $\boxed{70^\circ}$